Tips on Using BK-Trees

Introduction

A search facility on a website or in an application should be able to function when minor spelling errors are present in the text entered by the human user. The facility may either automatically execute the search, using the corrected words, or may return one
or more suggestions to the end user.

The Problem

Whilst a database index may store keys that enable millions of records to be swiftly retrieved by means of a perfect match between the entered text words and the contents of that database, providing means to retrieve data where minor spelling errors are present
cannot be satisfied by a regular database index. For example, the word Leicester should be returned if a user enters:-

1. liecester
2. leicestre
3. lecester

Each of the above entries contains a minor error, and entry (3) has a missing letter.

It will be noted from example (2) above, that one cannot assume that the first 3 or 4 letters are correct, and provide a wild card facility after the third or fourth character; this approach will limit the power of a fuzzy matching or spelling correction engine.

String Distance Calculations

Inherent in the solution presented below, is the ability to compute the difference between text strings as a numerical value, or distance.

I currently use the Levenshtein distance formula to calculate the distance between strings. The Levenshtein distance returns the number of changes required to transform string a to string b; for example the distance between ‘bristok’ and ‘bristol’ is 1 (change ‘k’ to ‘l’) and the distance between ‘bristle’ and ‘bristol’ is 2 (remove ‘e’ and insert ‘o’ before ‘l’).

BK-trees

The BK-tree was invented by Walter Austin Burkhard and Robert M. Keller. It is a metric tree specifically adapted to discrete metric spaces.

A loose description which is easier to understand is that the BK-tree is a means to greatly sub-divide a large ‘bag’ of objects into smaller collections in such a way that a search operation can easily find the correct collection and from there quickly find the desired matches.

Unlike a binary tree or a multi-branch B*Tree, a BK-tree is suitable to allow fuzzy string matching.

Creating a BK-tree

The creation of a BK-tree is quite simple. The root node is an arbitrary entry from our ‘bag’ of words. The actual strings are added as lowercase, and all searching would normally be case-insensitive.

Our words in this example, in no particular order, are:-

• Leeds
• York
• Bristol
• Leicester
• Hull
• Durham

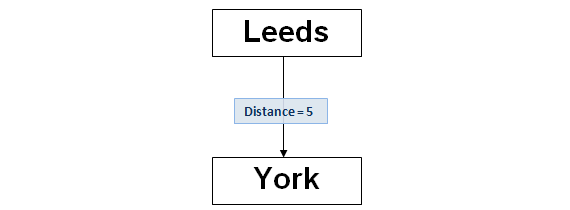
The root node is set to ‘Leeds’:-

The nodes can have multiple branches, each branch being a string distance value between the node’s text, and the text of the child node; this will be seen below.

To add the first child, ‘York’, calculate the string distance between it can the root node’s text, ‘Leeds’. The Levenshtein distance is 5. Create a child node with the value ‘York’, linked from the root node with a distance value of 5.

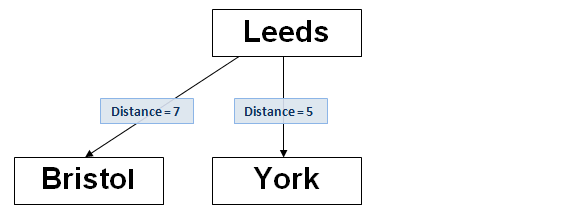
The next text to be added is ‘Bristol’. Repeating the procedure above by calculating the distance between ‘Bristol’ and ‘Leeds’, the value is 7.Next, check that there are no existing branches of value 7. There are none, so repeat the procedure as performed above, creating a new node and linking to the root node:-

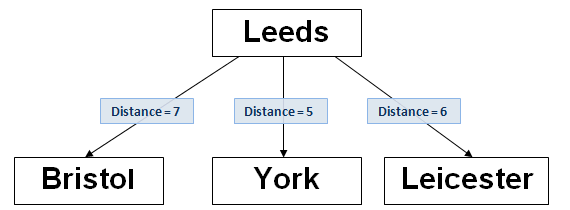
The fourth text to be added is ‘Leicester’. The procedure is identical to the second and third values, as above. The Levenshtein distance between ‘Leicester’ and the root node ‘Leeds’ is 6, so a new node is linked as shown below:-

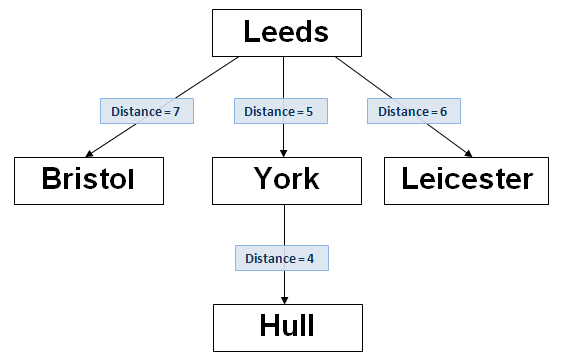
The next text value is ‘Hull’. Calculate the distance between ‘Hull’ and ‘Leeds’ ; it is 5. It will be noted that there is already a branch from the root node, of distance value 5. In this event, ‘move’ down that branch and repeat the insert procedure but compare the new text value to the current node, i.e. the one to which you have just moved, in this case,’York’. The Distance between ‘Hull’ and ‘York’ is 4, and as there are no branches from ‘York’ with distance=4, now add a new node as shown below:-

Note that if the ‘York’ branch already had a child to it with distance value 4, you would have moved down that branch to the child node, and repeated the above procedure until a node without a branch equal to the Levenshtein distance, is found.

Finally, add ‘Durham’ to the BK-tree, as illustrated below:-

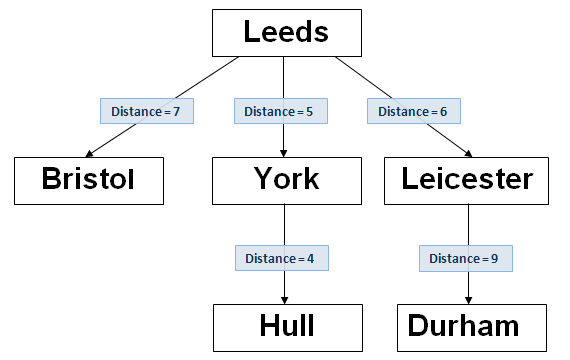
‘Durham’ had the Levenshtein distance from ‘Leeds’ of 6, so it was necessary to move down the branch to ‘Leicester’ and add it to that node.

The small BK-tree is now complete. Here’s how to search it.

Searching a BK-tree

The procedure for searching a BK-tree, to obtain a list of approximate matches to a word, is quite simple:-

• Set the ‘current node’ to the root node.
• Invoke a ‘search node’ function on the current node, passing the search word and maximum permitted Levenshtein distance from that word to the matches (max).
• The ‘search node’ function does the following:-
  1. Calculate dist = distance from the current node’s text to the search word.
  2. If dist <= max, add current node’s text to the final text list.
  3. Recursively invoke the search node function on any child nodes of the current node where the distance of the branch is in the inclusive range dist – max to dist + max.
• When the final invocation of the ‘search node’ function has returned, return the list of fuzzy matches found (if any).

A Worked Example

These are the detailed steps to search the above tree for the input text ‘Hill’ with a maximum allowed string distance of 1, for fuzzy matches to ‘Hill’.

The worked example is illustrated below. Note that the ‘Bristol’ branch from the root, which is not used during this search, is greyed out.

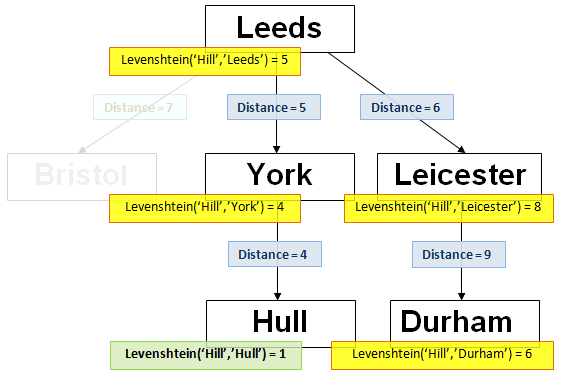
1. Set the current node to the root node ‘Leeds’.
2. Calculate the Levenshtein distance from the input text ‘Hill’ to the root node ‘Leeds’; the distance is 5.
3. If the distance is less than or equal to maximum allowed distance, add the current node’s text to the final text list; it is not.
4. Follow any branches from the current node, whose branch distance links are in the inclusive range distance – max to distance + max, in this case 4,5 and 6. There is no 4 branch, so go down the 5 and 6 branches.
5. It will be noted that the ‘Bristol’ branch is not used. Typically, at each node, one or more child branches are not followed.
6. Set the current node to ‘York’.
7. Repeat as at stage 2; calculate the distance between the search text ‘Hill’ and the current node ‘York’. The distance is 4. If the distance is less than or equal to max, add the current node’s text to the final list. Follow branches from the ‘York’ node in the range distance – max to distance + max, that is 3,4 and 5.
8. Follow any branches from ‘York’ with distances 3,4 and 5; there is only one, at distance 4. Set the current node to the ‘Hull’ node and execute the ‘search node’ function.
9. Repeat as at stage 2; calculate the distance between the search text ‘Hill’ and the current node’s text value ‘Hull’. The distance is 1, which is within the maximum allowed range, so add the current node’s text value ‘Hull’ to the final list.
10. There are no branches from the ‘Hull’ node, so exit the ‘search node’ function.
11. This will return the current node to the previous node, ‘York’. Follow any more branches in the range 3,4,5 (as at stage 8). There are none, so exit the ‘search node’ function.
12. This will return the current node to the previous node, the ‘Leeds’ node. Follow any further branches in the range 4,5 and 6 as stated at stage 4. The next branch to be followed is distance 6. Set the current node to ‘Leicester’, and invoke the ‘search node’ function.
13. Hopefully the next stage will be clear. Test the current node’s text against the search test, by calculating the Levenshtein distance. If the distance is 1 or less, add the current node’s text to the final list, and follow any child branches within the range as described above.
14. When the final invocation of ‘search node’ has completed, exit with the list of matches, in this case just a single match, ‘Hull’.