Shannon-Fano Compression in Native PHP

Shannon-Fano Compression in Native PHP
Shannon-Fano Compression explained and demonstrated
Introduction
This article will explain how Shannon-Fano coding works. Named after after Claude Shannon and Robert Fano, apart from run length encoding, this is probably the simplest form of lossless compression. I also include some PHP code to demonstrate compression and decompression natively. No deep knowledge of mathematics or compression is necessary, other than a basic knowledge of binary.About Compression
Compression is Everywhere
Just about everybody uses data compression today, probably without realising it. The DVD or Bluray that you watch, the MP3 you enjoy, and the digital TV that is now the only type in the UK, all use compression to reduce the size of the data that is stored or sent to you. The images on web pages, and sometimes even the web pages, are also compressed.Lossy Compression
The compression algorithms used by DVDs, Blurays, MP3s and some computer images (such as JPG files) use a form of compression called lossy simply because it does not reproduce he original data perfectly, it acheives a greater level of compression by removing the parts of the video, picture or sound that are not needed to enjoy the experience.Lossless Compression
Lossless compression is the counterpart to lossy - the original data is returned unchanged when the compressed data is uncompressed. If you extract files from a ZIP or RAR file, these are returned to you exactly as they were before they were added to the ZIP or RAR file. This article, and the article to follow, deal only with lossless compression.Compressing a Short Text Example
Let's start with a simple example. We will compress the word TATTOO. If we consider only a simple character string for the moment, TATTOO requires 6 bytes of storage. This article will show how TATTOO can be compressed into just 2 bytes using Shannon-Fano encoding. The detailed explanation of Shannon-Fano is below, but you don't need it yet. When a computer reads TATTOO from the 6 bytes of storage, it simply reads from the sequential bytes; each byte contains 8 bits of binary data. The binary representation of TATTOO is:-01010100 01000001 01010100 01010100 01001111 01001111..that is, 6 bytes or 48 binary bits. If we use Shannon-Fano to encode TATTOO, it is reduced to just:-
10011010 1...or just nine binary bits. The compressed data requires two bytes of storage (it almost fits into one). How is it done? Here's how.
Bits into Characters
The 9 bits 100110101 comprise the word TATTOO but unlike the uncompressed data, 8 bits does not represent a single character; the number of bits that represent each character is variable. That's how it compresses TATTOO into just 9 bits. You will see shortly that the 9 bit compressed data 100110101 comprises these bits to store the characters:-| BITS | Letter | |
|---|---|---|
| 1 | T | |
| 00 | A | |
| 1 | T | |
| 1 | T | |
| 01 | O | |
| 01 | O |
Binary Tree
The decompression software is supplied with a binary tree which it uses to decode the bitstream that is the compressed data. The decoder traverses the tree for once for each compressed element (character, in this instance). This is a simple and therefore fast operation for a computer to execute. A binary tree can be visualised by reference to the illustration below, showing the options to decode the first 3 binary digits of an encoded element. The tree is traversed by taking the left branch at each node if the current binary digit is 1, and the right branch if it's zero.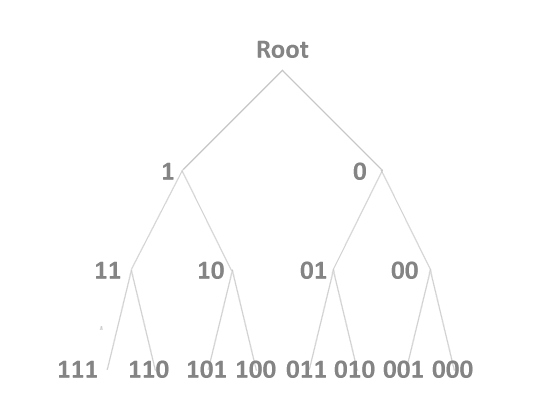
Using A Binary Tree to Decompress
Now we will use the actual binary tree which will be used to decompress the 9 bit compressed data sample. To decompress that data (100110101) we follow these steps. Please refer to the illustration below.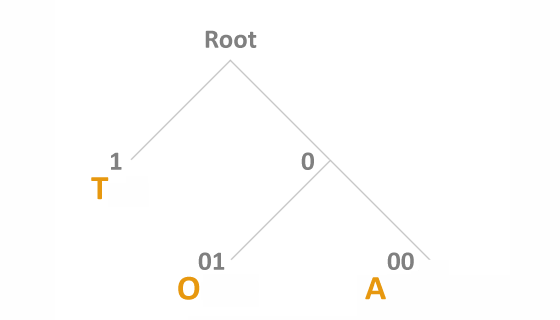
- Start at the Root, at the top.
- Read each compressed binary digit from left to right. The first digit is 1. If a digit is 1, take the left fork, and if it's 0 take the right.
- Moving from Root we thus branch left because the first digit is 1.
- If there are no futher branches possible from our new position, and there is data at that node (a leaf node), use the letter that is at the new position, as the first decoded character. It's T. Note that the illustration below also shows the binary bits that were used to decode this character, in this case just 1.
- After each character is decoded move back to Root. Read the next binary digit, which is 0. Take the right branch this time, from Root. If there are no further branches at the new position, use the letter; however this time, there are further branches.
- Read the next binary digit, 0. Again, move left for 1, or right for 0, so move right. At the new position you will see the numbers 00 which represents the bits you have used so far to decode this letter. We've arrived at a node which has no further branches but has a letter. We now have the second letter, A.
- Return to Root to decode the third character. The next bit is 1. Move left from Root to reach a node with no further branches and the letter T. We have character number 3.
- Repeat again,and once again we use the next bit which is 1; the movement down the tree gets the fourth character, T.
- The next bit is 0. Take the right branch from Root and then use the next bit, which is 1, and then take the next right fork to arrive the fifth letter, O.
- The final bits are 0 and 1, and you may have spotted that this is identical to the previous character; the sixth and final decoded character is O.
- We now have our complete decoded word, TATTOO, 48 bits extracted from just 9!
A Complete Compressed Message
When the source data is compressed, the software assigns the characters to be encoded, to the tree nodes, attempting to create a tree that will yield the most efficient compression of the source data. We have already seen an example of a compressed bitstream; the complete compressed data includes:-- The length of the uncompressed data
- Data telling how to construct the binary tree that was used to compress the data
- The compressed data
Creating the Binary Tree using Shannon-Fano
The Shannon-Fano algorithm used to create the binary tree to compress and decompress is very simple.- Create a empty binary tree. Set the current position to the root
- Create a frequency table for all elements present in the source data
- Sort the table by frequency so that the most common element is at the start
- Split the table so that the total frequencies in both parts are as close as can be. The most common symbols are in the "left" portion, the least in the "right". You now have two parts.
- Work on each part. Split the part so that the total frequencies in both parts are as close as can be.
- Repeat 5 until the part has 2 or less symbols.
- Assign digits for each part; the left portion is assign 1, the right is assigned 0
- Repeat for all parts.
| Symbol | Frequency> |
|---|---|
| T | 3 |
| O | 2 |
| A | 1 |
Compressing Data using the Binary Tree
Compression is the reverse of the decompression process explained earlier. Using a binary tree created as above, do this for each character in the uncompressed text:-- Find the leaf node for the current character.
- Work from that node up to the root. Repeat 2 until you are at the root (recursively).
- Add a 1 to the final output if your move up was from the left branch, 0 if from the right. Repeat 3 until all calls at 2 are done.
There is, However, One Small Problem
Shannon-Fano is not very good. The algorithm to assign the bits to symbols does not produce the best compression results. Shannon-Fano is generally not used now; Huffman coding and other methods have replaced it.Using Shannon-Fano (Regardless) for PHP
If you would like to use Shannon-Fano in PHP, we have prepared a PHP class which compresses and decompresses text in memory. It was created as a means to demonstrate Shannon-Fano, but it could be utilised. Typical uses could be:-- Storing large text in a database BLOB in a compressed form.
- Compressing binary data.
Our PHP Class Shannon.php
The class has just four public functions:-- compressText which as its name implies, compresses text, producing a byte array.
- expandText which expands a byte array that was previously compressed from text
- compressBin which compresses a byte array, producing another byte array.
- expandBin which expands a byte array that was previously compressed from a byte array
<!--?php require('Shannon.php'); $instance = new Shannon(); $text = "More ending in death, but this time it sounds like a "; $text.= "solace after life. I lingered round them, under that "; $text.= "benign sky; watched the moths fluttering among the "; $text.= "heath, and hare-bells; listened to the soft wind "; $text.= "breathing through the grass; and wondered how any one "; $text.= "could ever imagine unquiet slumbers "; $text.= "for the sleepers in that quiet earth."; echo "text len=".strlen($text)." characters\n"; $enc_ar = $instance -> compressText($text);
echo "encoded len=".count($enc_ar)." bytes\n";
$org_text = $instance -> expandText($enc_ar);
if(strcmp($org_text,$text)==0)
{
echo "decoded text matches\n";
}
else
{
echo "decoded text DOES NOT match\n";
}
?-->
The above text (the end of Wuthering Heights) comprises 333 characters. The resulting compressed byte array is 227 bytes in length
The PHP class is available to download here.
Beyond Shanon-Fano
A forthcoming blog post will explain and demonstrate Huffman coding, a similar but more efficient method.
- compressText which as its name implies, compresses text, producing a byte array.
- expandText which expands a byte array that was previously compressed.